En muchas ocasiones se presenta el cálculo de límites de cocientes, diferencias y productos de funciones en los que al reemplazar la variable por el valor al cual tiende se generan indeterminaciones del tipo 
. El resultado de estos límites no puede anticiparse y el mismo puede ser cero, ¥ , -¥ , un número finito diferente de cero, o bien puede no existir. Para resolverlos, se realizan procedimientos algebraicos adecuados que permitan salvar la indeterminación.
Para resolver:
La indeterminación 
Para salvar indeterminaciones de este tipo, es posible reducir el cociente planteado a otro cuyo denominador no sea cero factorizando el numerador y/o el denominador, cancelando luego los factores comunes. En otras ocasiones, es posible crear un factor común multiplicando el numerador y el denominador por la expresión conjugada de la que se presenta en uno de ellos.
Ejemplo. Halle 
Al sustituir, resulta 
y 
lo que genera una indeterminación del tipo 
.
Sin embargo, como 
si x ¹ 3, resulta que la función 
coincide con la función (x + 3) salvo en x = 3.
Como interesa analizar el comportamiento de la función para valores de x próximos a 3 (por izquierda y por derecha), es posible determinar el comportamiento de analizando el de la función (x + 3).
Por lo tanto puede decirse que 
La indeterminación 
Se analizará el límite del cociente de dos funciones polinomiales en el que la variable crece o decrece indefinidamente. Se debe tener en cuenta que el límite de una función polinomial de grado n ³ 1 cuando x tiende a +¥ ó a -¥ es +¥ ó -¥ . Para resolver límites de este tipo, se dividen el numerador y el denominador de la función dada por xn, siendo n el mayor de los grados de las funciones polinomiales. Luego se aplican las propiedades de los límites.
Ejemplo. Halle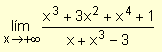 
La función dada consiste en el cociente de dos funciones polinomiales: una de grado 4 y otra de grado 3. Por lo tanto, se dividen el numerador y el denominador por x4 y resulta:
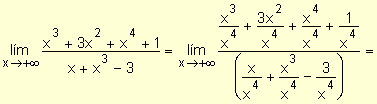
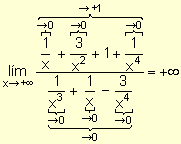
En el ejemplo dado, el grado de la función polinomial del numerador es mayor que el de la del denominador y se obtuvo en este caso ¥.
La indeterminación 
Los procedimientos algebraicos para salvar una indeterminación de este tipo, se desarrollan en los siguientes ejemplos:
Ejemplo. Determine el valor de 
.
Al reemplazar la variable por 2 resulta ¥ -¥ , que es una indeterminación.
Resolviendo la diferencia se obtiene:
Cuando x se aproxima a 2 por derecha, el numerador tiende a –3 y el denominador a 0 por valores mayores que él. Por lo tanto, la expresión resulta negativa y el límite es -¥.
= -¥
Tomado de: https://www.fca.unl.edu.ar/Limite/2.4%20Limites%20indeterminados.htm
