Limites al infinito

Limites al infinito
 
Definición
 

Sea $f$ una función con dominio $k$ tal que para cualquier número $c$ existen elementos de $k$ en el intervalo $[c,+\infty[$.

El límite de $f(x)$ cuando $x$ tiende a más infinito es $L$, que se representa$\displaystyle {\lim_{x \rightarrow{+\infty}}{f(x)}=L}$, si para cada $\varepsilon >0$ existe un número $M$ tal que $\vert f(x)-L\vert<\varepsilon$para toda $x\in k$ y $x>M$.

 

 

Ejemplo

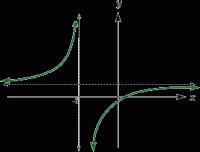
Probar que $\displaystyle {\lim_{x \rightarrow{+\infty}}{\frac{x}{x+2}}=1}$

Hay que demostrar que para $\varepsilon >0$ existe $M$ tal que $\displaystyle {\left\vert\frac{x}{x+2}-1\right\vert<\varepsilon}$ si$x>M,\;\;e\in I\!\!R-\{2\}$

Se tiene que $\displaystyle {\left\vert\frac{x}{x+2}-1\right\vert=\left\vert\frac{x-x-2}{x+2}\right\vert=\left\vert\frac{-2}{x+2}\right\vert=\frac{2}{\vert x+2\vert}}$

Si $x>-2$ entonces $\vert x+2\vert=x+2$ por lo que: 

$\displaystyle {\left\vert\frac{x}{x+2}-1\right\vert=\frac{2}{x+2}}$

Luego, dada $\varepsilon >0$ se cumple que $\displaystyle {\left\vert\frac{x}{x+2}-1\right\vert<\varepsilon}$ si y solo si $\displaystyle\frac{2}{x+2}<\varepsilon$, o sea, si$x>\displaystyle {\frac{2}{\varepsilon}-2}$, por lo que podemos tomar $M=\displaystyle {\frac{2}{\varepsilon}-2}$ de tal forma que se verifique que$\left\vert\displaystyle\frac{x}{x+2}-1\right\vert<\varepsilon$ siempre que $x>M$. 

Por ejemplo, si $\varepsilon =\displaystyle {\frac{1}{2}}$ entonces $M=2$ por lo que: 

$\left\vert\displaystyle\frac{x}{x+2}-1\right\vert<\displaystyle {\frac{1}{2}}\;\;\mbox{si}\;\;x>2$

La representación gráfica de la función es la siguiente:


 
 
  Definición
 

Sea $f$ una función con dominio $k$ tal que para cualquier número $c$, existen elementos de $k$ en el intervalo $]-\infty,c]$. 
El límite de $f(x)$ cuando $x$ tiende a menos infinito es $L$, que se representa$\displaystyle {\lim_{x \rightarrow{-\infty}}{f(x)}=L}$, si para todo $\varepsilon >0$ existe un número $M$ tal que $\vert f(x)-L\vert<\varepsilon$para cada $x \in K$ y $x<M$.

Tomado de: https://www.tec-digital.itcr.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/limitesycontinuidad/html/node11.html